Относительная и абсолютная погрешность – формула определения, как рассчитать погрешность измерения

Абсолютная погрешность
Абсолютной погрешностью числа называют разницу между этим числом и его точным значением.
Рассмотрим пример: в школе учится 374 ученика. Если округлить это число до 400, то абсолютная погрешность измерения равна 400-374=26.
Для подсчета абсолютной погрешности необходимо из большего числа вычитать меньшее.
Существует формула абсолютной погрешности. Обозначим точное число буквой А, а буквой а – приближение к точному числу. Приближенное число – это число, которое незначительно отличается от точного и обычно заменяет его в вычислениях. Тогда формула будет выглядеть следующим образом:
Δа=А-а. Как найти абсолютную погрешность по формуле, мы рассмотрели выше.
На пpaктике абсолютной погрешности недостаточно для точной оценки измерения. Редко когда можно точно знать значение измеряемой величины, чтобы рассчитать абсолютную погрешность. Измеряя книгу в 20 см длиной и допустив погрешность в 1 см, можно считать измерение с большой ошибкой. Но если погрешность в 1 см была допущена при измерении стены в 20 метров, это измерение можно считать максимально точным. Поэтому в пpaктике более важное значение имеет определение относительной погрешности измерения.
Записывают абсолютную погрешность числа, используя знак ±. Например, длина рулона обоев составляет 30 м ± 3 см. Границу абсолютной погрешности называют предельной абсолютной погрешностью.
Относительная погрешность
Относительной погрешностью называют отношение абсолютной погрешности числа к самому этому числу. Чтобы рассчитать относительную погрешность в примере с учениками, разделим 26 на 374. Получим число 0,0695, переведем в проценты и получим 6%. Относительную погрешность обозначают процентами, потому что это безразмерная величина. Относительная погрешность – это точная оценка ошибки измерений. Если взять абсолютную погрешность в 1 см при измерении длины отрезков 10 см и 10 м, то относительные погрешности будут соответственно равны 10% и 0,1%. Для отрезка длиной в 10 см погрешность в 1см очень велика, это ошибка в 10%. А для десятиметрового отрезка 1 см не имеет значения, всего 0,1%.
Различают систематические и случайные погрешности. Систематической называют ту погрешность, которая остается неизменной при повторных измерениях. Случайная погрешность возникает в результате воздействия на процесс измерения внешних факторов и может изменять свое значение.
Правила подсчета погрешностей
Для номинальной оценки погрешностей существует несколько правил:
- при сложении и вычитании чисел необходимо складывать их абсолютные погрешности;
- при делении и умножении чисел требуется сложить относительные погрешности;
- при возведении в степень относительную погрешность умножают на показатель степени.
Приближенные и точные числа записываются при помощи десятичных дробей. Берется только среднее значение, поскольку точное может быть бесконечно длинным. Чтобы понять, как записывать эти числа, необходимо узнать о верных и сомнительных цифрах.
Верными называются такие цифры, разряд которых превосходит абсолютную погрешность числа. Если же разряд цифры меньше абсолютной погрешности, она называется сомнительной. Например, для дроби 3,6714 с погрешностью 0,002 верными будут цифры 3,6,7, а сомнительными – 1 и 4. В записи приближенного числа оставляют только верные цифры. Дробь в этом случае будет выглядеть таким образом – 3,67.
Что мы узнали?
Абсолютные и относительные погрешности используются для оценки точности измерений. Абсолютной погрешностью называют разницу между точным и приближенным числом. Относительная погрешность – это отношение абсолютной погрешности числа к самому числу. На пpaктике используют относительную погрешность, так как она является более точной.
Еще:
-1 ::




 Рюкзак со светящимся экраном, на который можно закачать свою картинку
Рюкзак со светящимся экраном, на который можно закачать свою картинку
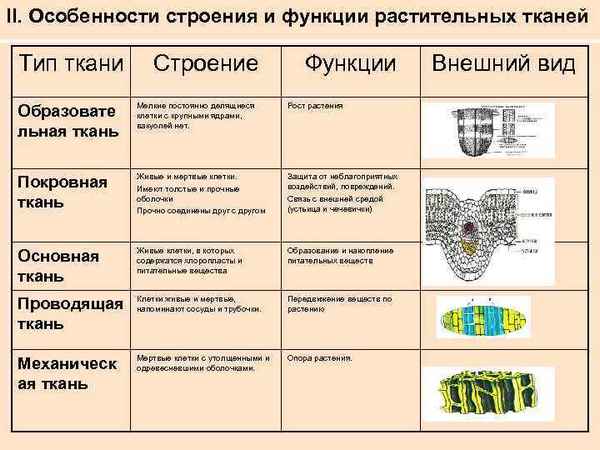 Виды тканей растений (Биология) и их функции, таблица для 6 класса
Виды тканей растений (Биология) и их функции, таблица для 6 класса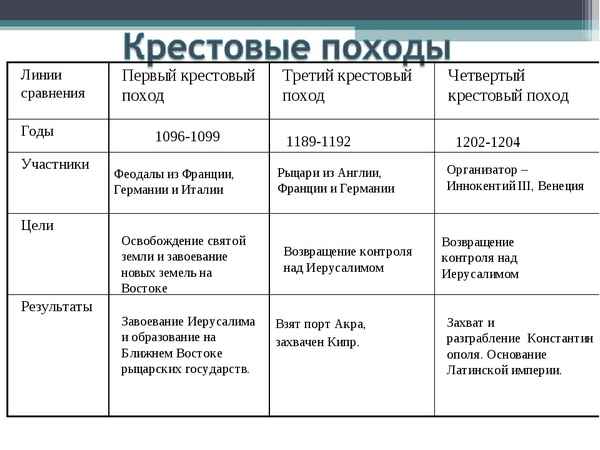 Крестовые походы кратко в таблице – страны, города, даты (история, 6 класс)
Крестовые походы кратко в таблице – страны, города, даты (история, 6 класс)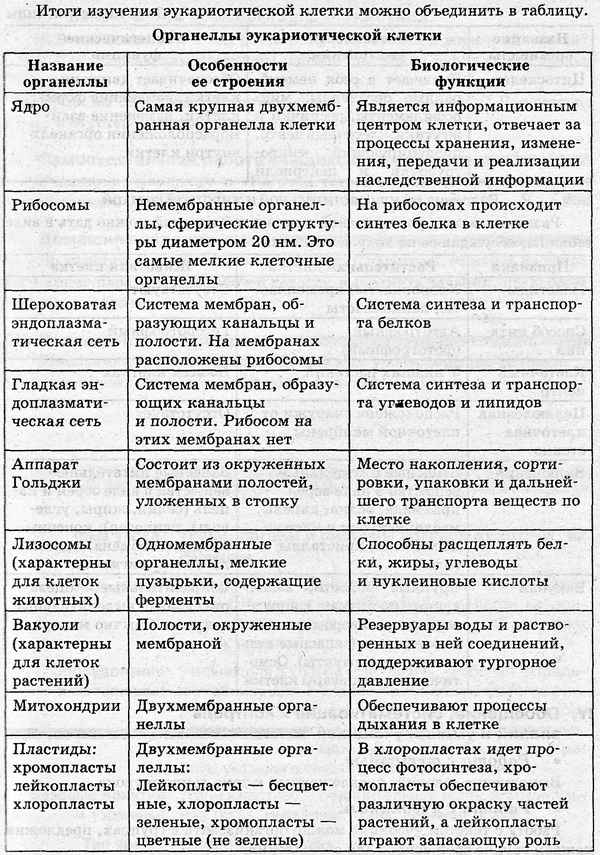 Строение эукариотической клетки в таблице, кратко о функциях (9 класс, биология)
Строение эукариотической клетки в таблице, кратко о функциях (9 класс, биология)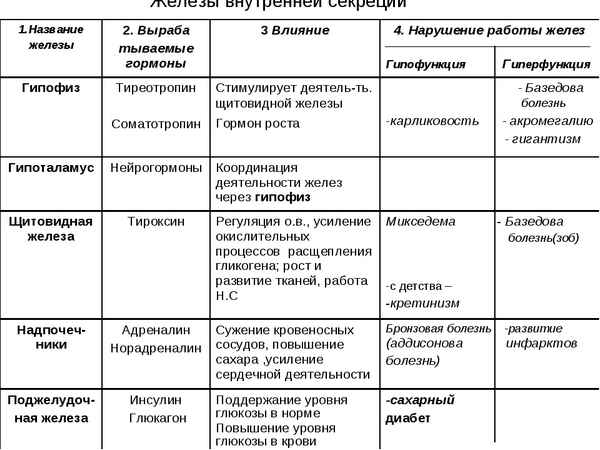 Железы внутренней секреции человека в таблице
Железы внутренней секреции человека в таблице Проливы и заливы России – список, описание и карта
Проливы и заливы России – список, описание и карта Самая краткая биография Рахманинова
Самая краткая биография Рахманинова Крупные морские порты Зарубежной Европы, главные мировые приморские страны
Крупные морские порты Зарубежной Европы, главные мировые приморские страны Стадии антропогенеза в таблице (11 класс, биология)
Стадии антропогенеза в таблице (11 класс, биология) Клеточный центр – строение и функции в таблице
Клеточный центр – строение и функции в таблице Строение скелета человека в таблице (8 класс, биология)
Строение скелета человека в таблице (8 класс, биология)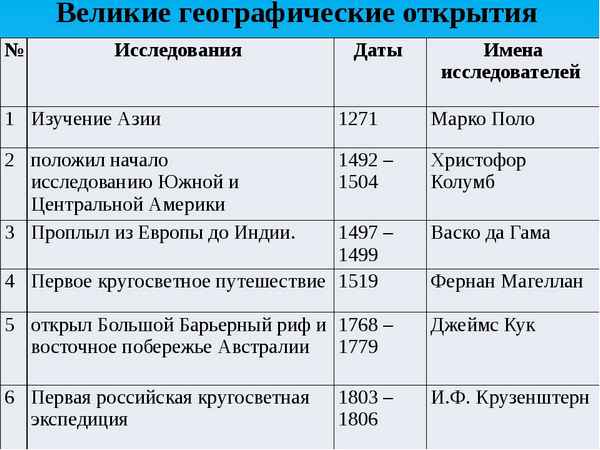 Великие географические открытия и путешественники – кратко о периоде
Великие географические открытия и путешественники – кратко о периоде Особенности строения и жизнедеятельности клеток, основные проявления процесса
Особенности строения и жизнедеятельности клеток, основные проявления процесса Самая краткая биография Глинки
Самая краткая биография Глинки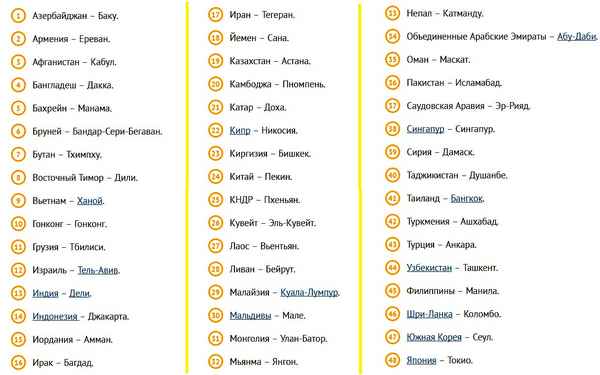 Страны Азии и их столицы – список и таблица
Страны Азии и их столицы – список и таблица Самая краткая биография Грибоедова
Самая краткая биография Грибоедова Краткая биография Крылова творчество баснописца Ивана Андреевича – самое главное и важное для детей
Краткая биография Крылова творчество баснописца Ивана Андреевича – самое главное и важное для детей Краткая биография Тургенева самое главное и интересные факты творчества Иван Сергеевича
Краткая биография Тургенева самое главное и интересные факты творчества Иван Сергеевича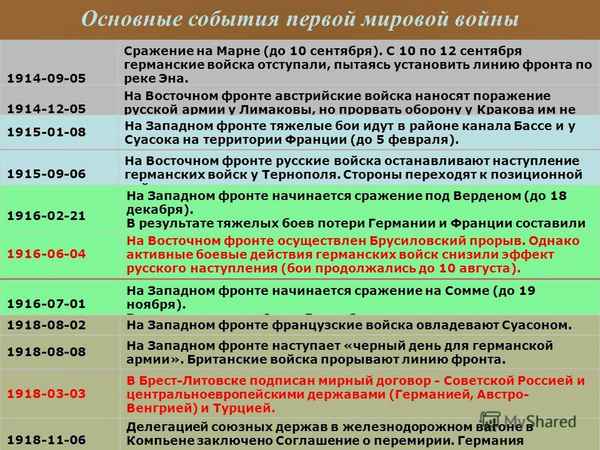 Основные события Первой мировой войны – хронология в таблице
Основные события Первой мировой войны – хронология в таблице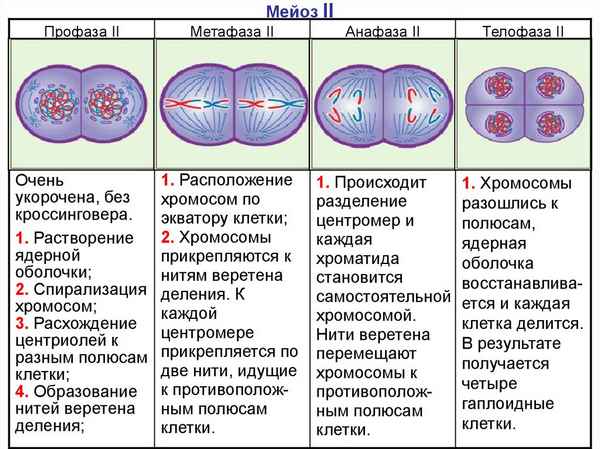 Мейоз – фазы, кратко и понятно о первом и втором делении, стадии
Мейоз – фазы, кратко и понятно о первом и втором делении, стадии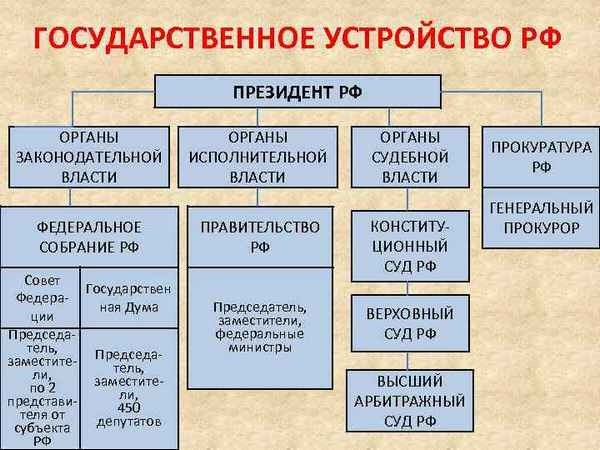 Государственное устройство России – форма и основы в 20 веке
Государственное устройство России – форма и основы в 20 веке Краткая биография Лермонтова, самое главное и краткое содержание жизни Михаила Юрьевича для всех классов
Краткая биография Лермонтова, самое главное и краткое содержание жизни Михаила Юрьевича для всех классов Самая краткая биография Невского
Самая краткая биография Невского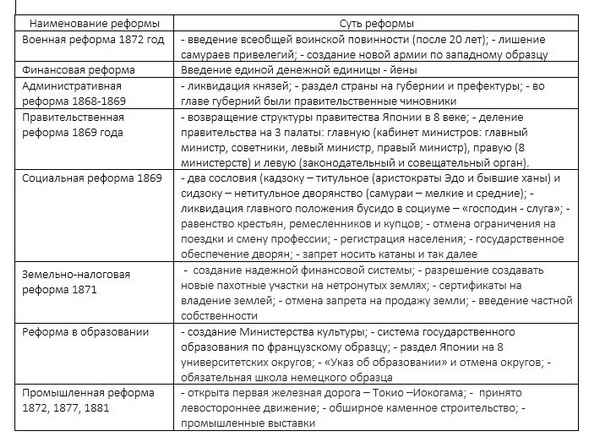 Япония на пути модернизации кратко в таблице (история, 8 класс)
Япония на пути модернизации кратко в таблице (история, 8 класс)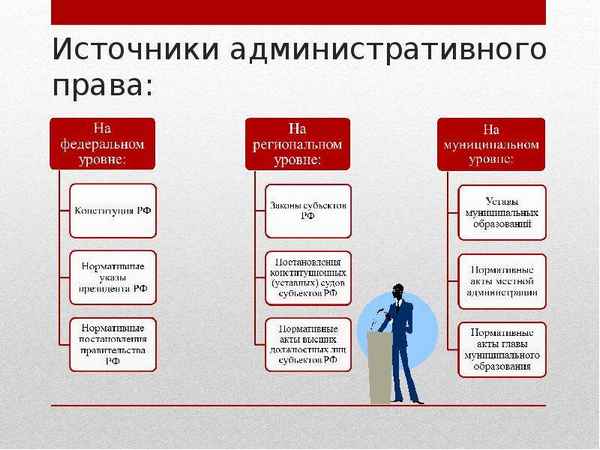 Источники административного права в РФ – виды и понятие
Источники административного права в РФ – виды и понятие Краткая биография Глинка интересное о композиторе Михаиле Ивановиче для детей
Краткая биография Глинка интересное о композиторе Михаиле Ивановиче для детей Краткая биография Некрасова, самое главное в жизни и творчестве Николая Алексеевича
Краткая биография Некрасова, самое главное в жизни и творчестве Николая Алексеевича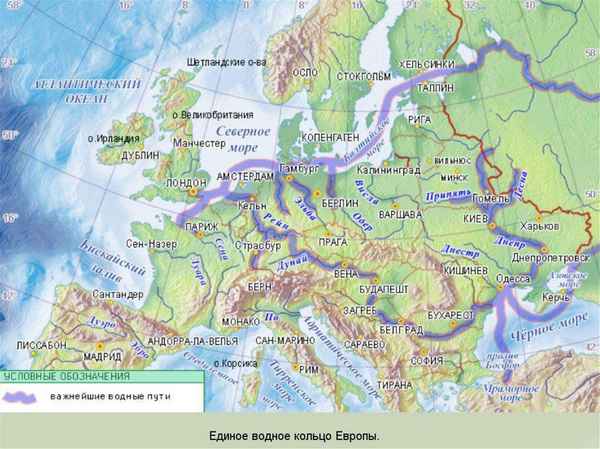 Реки Зарубежной Европы – крупные и самые длинные судоходные реки на карте
Реки Зарубежной Европы – крупные и самые длинные судоходные реки на карте Биография Гончарова кратко – самое главное и интересные факты из жизни и творчества Иван Александровича
Биография Гончарова кратко – самое главное и интересные факты из жизни и творчества Иван Александровича Причастие и деепричастие – правила с примерами в русском языке
Причастие и деепричастие – правила с примерами в русском языке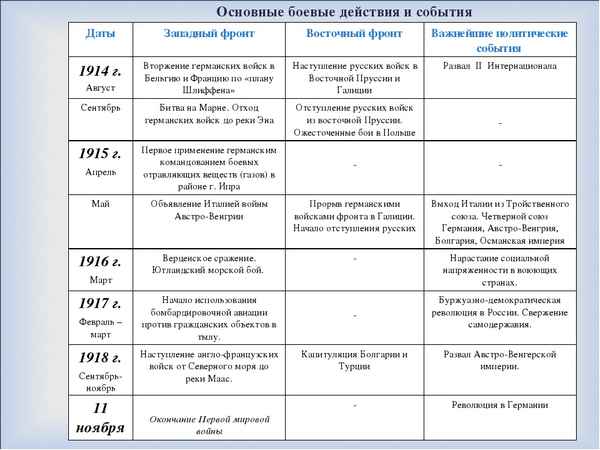 Основные сражения Первой мировой войны в таблице – морские и военные
Основные сражения Первой мировой войны в таблице – морские и военные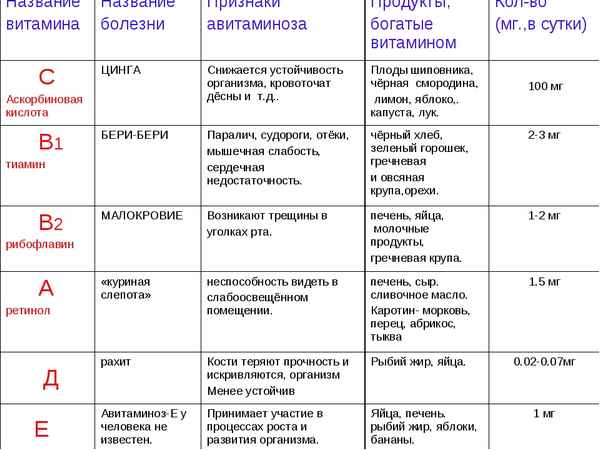 Витамины (таблица по биологии, 8 класс)
Витамины (таблица по биологии, 8 класс)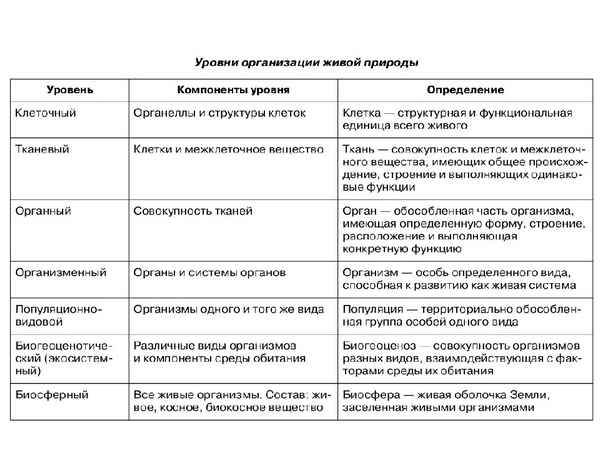 Уровни организации живой природы: таблица свойства живых организмов
Уровни организации живой природы: таблица свойства живых организмов Признаки глагола и прилагательного у причастия
Признаки глагола и прилагательного у причастия Истории различных видов трaнcпорта (2 класс, окружающий мир)
Истории различных видов трaнcпорта (2 класс, окружающий мир)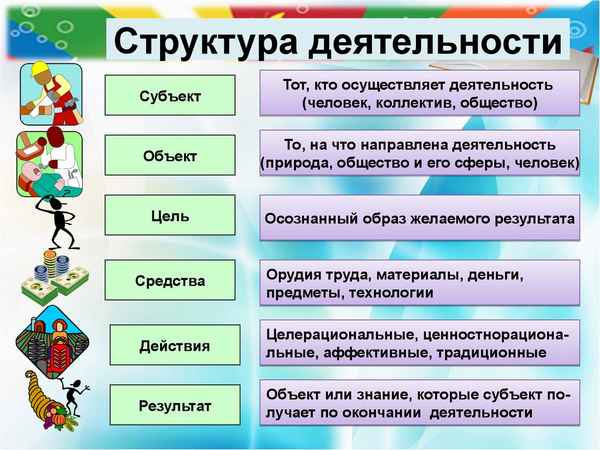 Структура деятельности – специфика в поведении, познавательная деятельность (обществознание, 10 класс)
Структура деятельности – специфика в поведении, познавательная деятельность (обществознание, 10 класс) Суффиксы причастий и деепричастий – таблица
Суффиксы причастий и деепричастий – таблица Пит Роуз (Pete Rose) краткая биография бейсболиста
Пит Роуз (Pete Rose) краткая биография бейсболиста Морфологический разбор причастия – примеры морфемного разбора слова по составу
Морфологический разбор причастия – примеры морфемного разбора слова по составу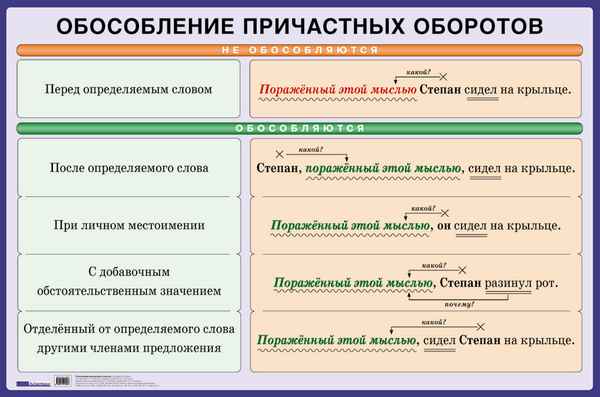 Обособление причастий и причастного оборота, правила для сложных случаев
Обособление причастий и причастного оборота, правила для сложных случаев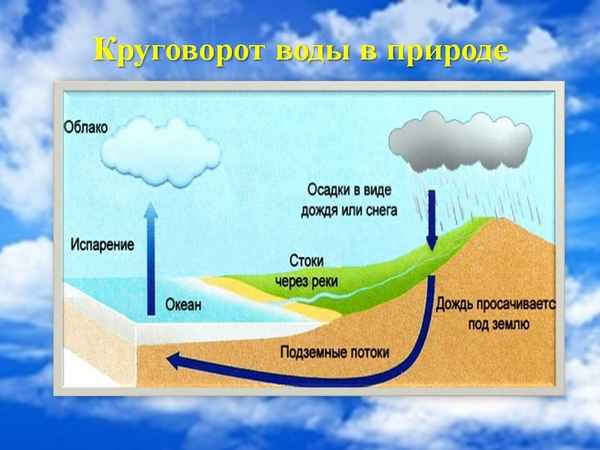 Круговорот воды в природе – схема превращения, кратко как происходит
Круговорот воды в природе – схема превращения, кратко как происходит Русско-японская война 1904-1905 гг кратко даты и события в таблице
Русско-японская война 1904-1905 гг кратко даты и события в таблице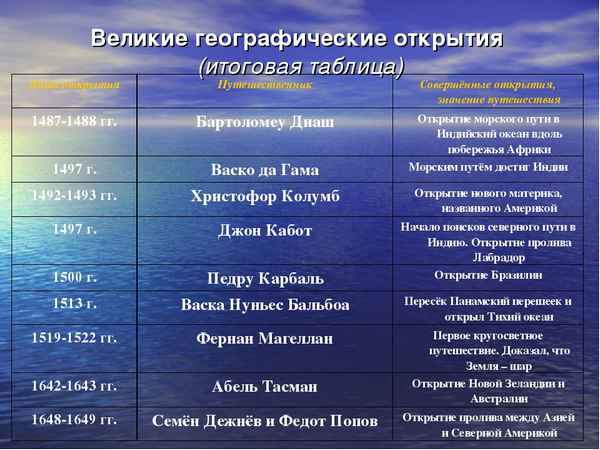 Великие географические открытия и имена путешественников – кратко о периоде истории (7 класс)
Великие географические открытия и имена путешественников – кратко о периоде истории (7 класс) Краткая биография Карамзина – творчество поэта и историка Николая Михайловича, самое главное
Краткая биография Карамзина – творчество поэта и историка Николая Михайловича, самое главное