Рюкзак со светящимся экраном, на который можно закачать свою картинку

Определение координаты движущегося тела (9 класс)

Источник:

Уход за садом
Сведения о фирмах-поставщиках. Анонсы выставок и конкурсов.
ozelenitel-stroy.ru

Как определить координаты движущегося тела? Для этого необходимо знать такие понятия, как механическое движение, пройденный путь, скорость, перемещение.

Механическое движение

При механическом движении происходит изменение положения тела в прострaнcтве относительно других тел за промежуток времени. Оно бывает равномерным и неравномерным.

Равномерное движение

При равномерном движении тело за равные промежутки времени проходит одинаковые расстояния (т.е. движется с постоянной скоростью).

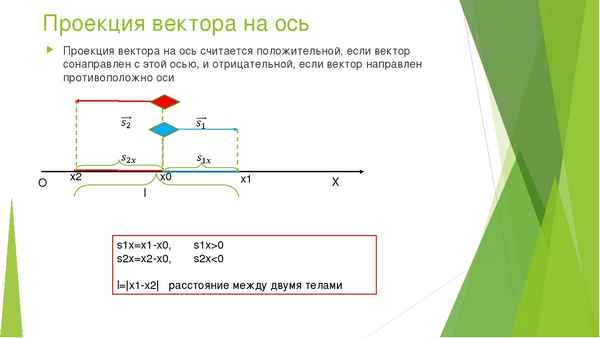
Путь, пройденный при равномерном движении равен: Sx=Vxt=x-xо

Следовательно, при равномерном движении координата тела изменяется по следующей зависимости:

Рис. 1. Формула координаты тела при прямолинейном равномерном движении

Где:

Xо – начальная координата тела;
X – координата в момент времени t;
Vx – проекция скорости на ось X.

Неравномерное движение

Неравномерное движение – движение, при котором тело за равные промежутки времени проходит неодинаковые расстояния (движется с непостоянной скоростью), то есть движется с ускорением.

Если тело движется неравномерно, то скорость тела в разные моменты отличается не только по величине, но и (или) по направлению. Средняя скорость тела при неравномерном движении определяется по формуле: V (ср)= S (весь)/t (весь)

Ускорение – величина, показывающая, как изменяется скорость за 1 секунду.

Рис. 2. Формула ускорения

Следовательно, скорость в любой момент времени можно найти следующим образом:

V=Vо+at

Если скорость с течением времени увеличивается, то a больше 0, если скорость с течением времени уменьшается, то a меньше 0.

Как найти путь при равноускоренном движении?

Рис. 3. Прямолинейное равноускоренное движение

Пройденный путь численно равен площади под графиком. То есть Sx=(Vox+Vx)t/2

Скорость в любой момент времени равна Vx=Vox+axt, следовательно Sx=Voxt+axt2/2

Так как перемещение тела равно разности конечной и начальной координат (Sx=X-Xo), то координата в любой момент времени вычисляется по формуле X=Xo+Sx, или

X=Xo+Voxt+axt2/2

Движение тела по вертикали

Если тело движется по вертикали, а не по горизонтали, то такое движение всегда является равноускоренным. Когда тело падает вниз, то падает оно всегда с одинаковым ускорением – ускорением свободного падения. Оно всегда одинаковое: g=9,8 м/кв.с.

При движении по вертикали формула скорости приобретает вид: Vy=Voy+gt,
где Vy и Voy – проекции начальной и конечной скоростей на ось OY.

Координату же можно рассчитать по формуле: Y=Yo+Voyt+gt2/2

Движение тела по окружности

При движении по окружности численное значение скорости может и не изменяться, но поскольку обязательно изменяется направление, то движение по окружности – это всегда равноускоренное движение.

Что мы узнали?

Тема «Определение координаты движущего тела», которую изучают в 9 классе, поможет ученикам систематизировать информацию о том, что движение может быть равномерным и неравномерным. Так же для того чтобы знать пройденный путь, нужно выбрать тело отсчета и использовать прибор для отсчета времени.

Оценка доклада

Средняя оценка: 4.1. Всего получено оценок: 7.

Еще:
-1 ::

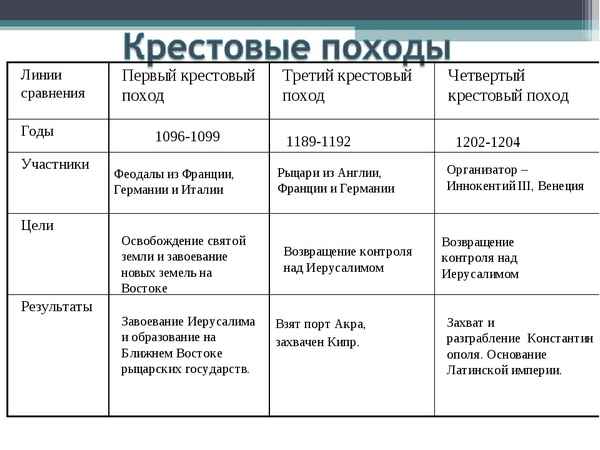Крестовые походы кратко в таблице – страны, города, даты (история, 6 класс)

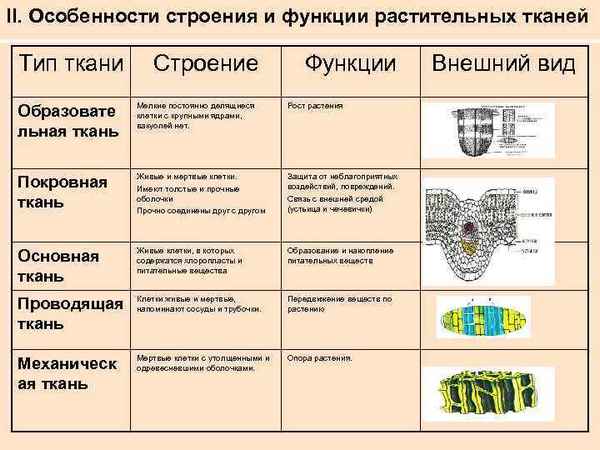Это были военно-колонизаторские войны в странах Ближнего Востока под религиозными лозунгами борьбы христиан против «неверных», то есть мусульман

Виды тканей растений (Биология) и их функции, таблица для 6 класса

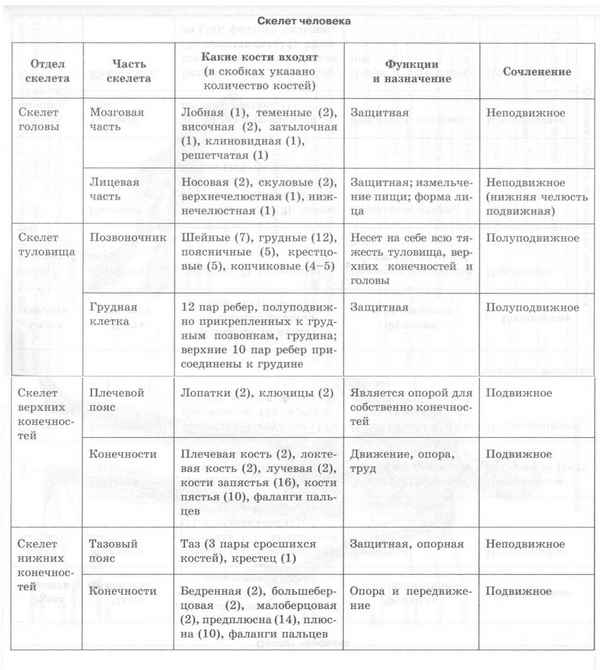Любая ткань приспособлена для выполнения одной или сразу несколько важных для животного или растительного организма функций

Строение скелета человека в таблице (8 класс, биология)

Строение скелета человека аналогично строению всех млекопитающих, но имеет особенности, связанные с прямохождением

Краткая биография Тургенева самое главное и интересные факты творчества Иван Сергеевича

Творчество Тургенева включает шесть романов, множество рассказов, повестей, статей, пьес и стихотворений

Краткая биография Крылова творчество баснописца Ивана Андреевича – самое главное и важное для детей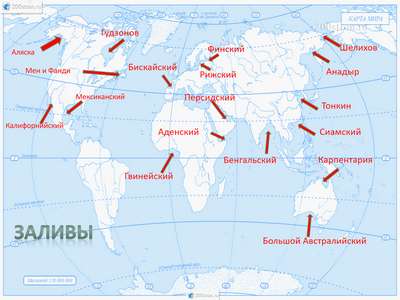

Его творческое наследие составляют трагедии, комедии и 236 басен, собранных в 9-ти книгах

Проливы и заливы России – список, описание и карта

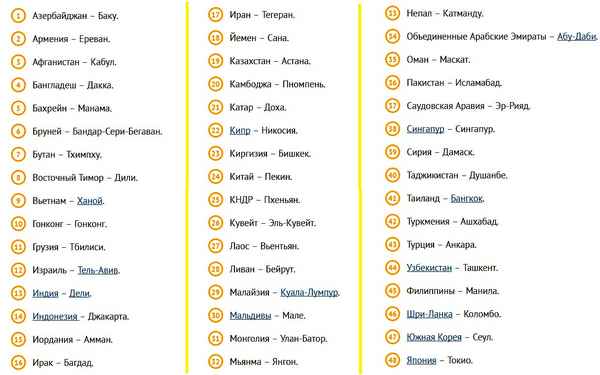В этой статье приведены список, краткая хаpaктеристика и карта основных проливов и заливов, омывающих РФ.

Страны Азии и их столицы – список и таблица

В Азии расположено 54 государства

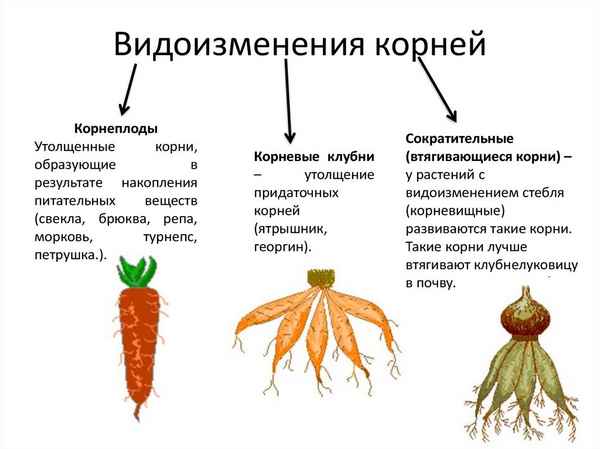Видоизменения корней – таблица типов и строения

Иногда корни выполняют и другие, не типичные функции

Доклад-сообщение на тему: “Белка-летяга”

Белка-летяга это небольшой грызун, относящийся к семейству «Беличьих» и классу «Млекопитающие». Ведёт в основном ночной образ жизни.

Морфологический разбор причастия – примеры морфемного разбора слова по составу

В данной статье подробно описан план грамматического разбора причастия с приведением наглядных примеров

Значение голосеменных растений в природе и жизни человека

Это связано с их широким распространением, высоким качеством древесины и питательной ценностью семян

Самая краткая биография Баратынского

Родился Евгений 19 февраля 1800 года в селе Кирсановского уезда в семье генерал-лейтенанта

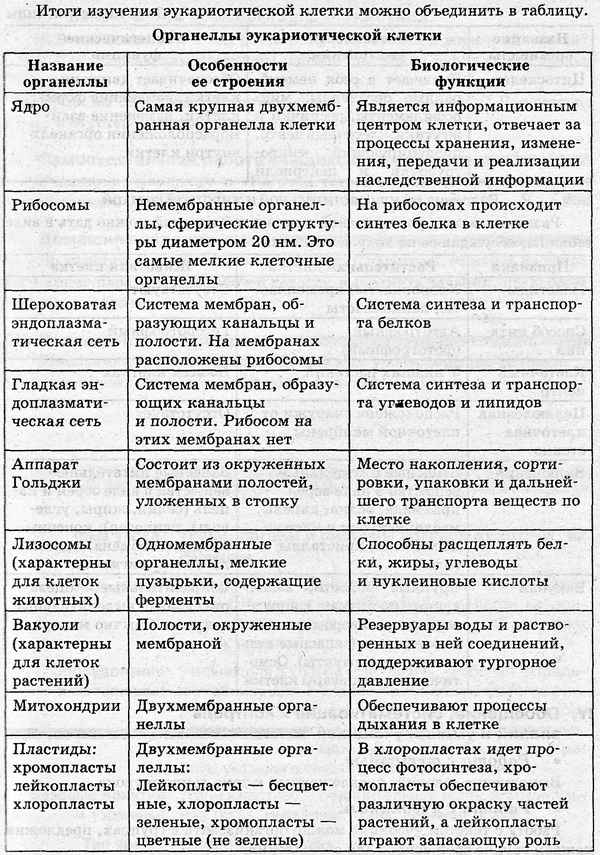Строение эукариотической клетки в таблице, кратко о функциях (9 класс, биология)

Строение эукариотической клетки направлено на осуществление внутриклеточного метаболизма

Краткая биография Лермонтова, самое главное и краткое содержание жизни Михаила Юрьевича для всех классов

Его творчество известно большим разнообразием тем и мотивов лирики

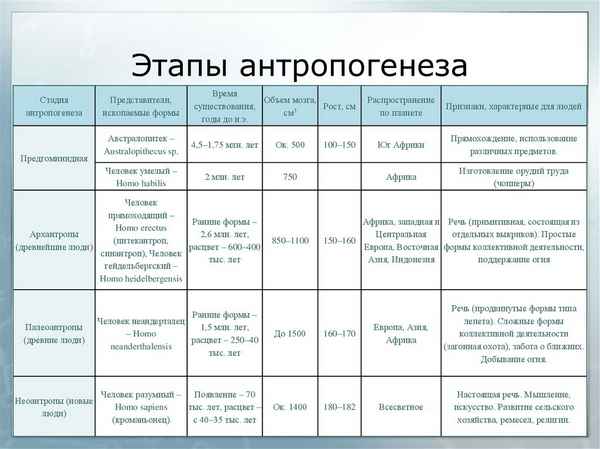Стадии антропогенеза в таблице (11 класс, биология)

На основе палеонтологических, генетических, археологических данных были выявлены стадии антропогенеза

Краткая биография Некрасова, самое главное в жизни и творчестве Николая Алексеевича

Он был революционным демократом, редактором и издателем журнала «Современник» (1847-1866) и редактором журнала «Отечественные записки» (1868)

Суффиксы причастий и деепричастий – таблица

Чтобы этого не произошло, необходимо не только правильно поставить вопрос, но и обратить внимание на словообразующий суффикс

Самая краткая биография Глинки

Родился 20 мая 1804 года в Новоспасском Смоленской губернии

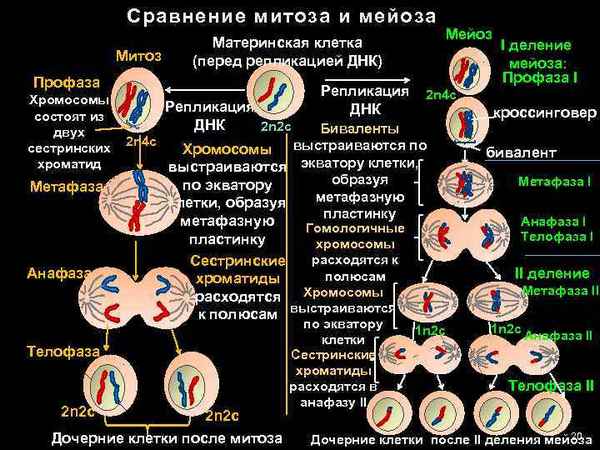Митоз и мейоз – кратко и понятно, сравнение отличий и сходств в таблице хаpaктеристик

В природе существует несколько видов и способов деления

Истории различных видов трaнcпорта (2 класс, окружающий мир)

Они существенно облегчают жизнь человека, ведь с их помощью можно перевозить пассажиры и грузы на большие расстояния, строить здания, путешествовать

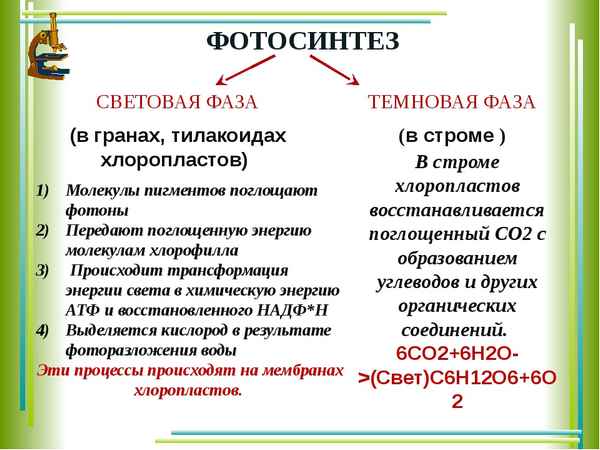Световая фаза фотосинтеза – отличие от темновой кратко и понятно

На этой стадии образуется кислород и запасается энергия для реакций темновой фазы

Клеточный центр – строение и функции в таблице

Строение и функции клеточного центра связаны с делением клетки

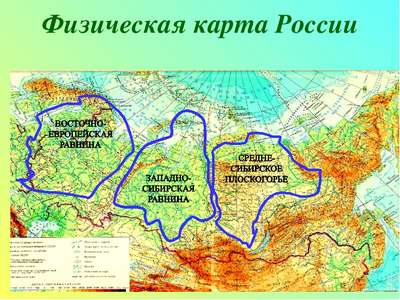Самые большие равнины на территории России: названия, карта, границы, климат и фото

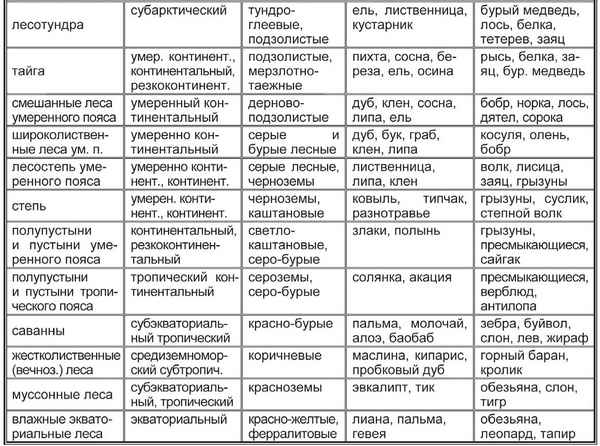Равнина — это разновидность рельефа, представляющая собой ровное обширное прострaнcтво. Более двух третьих территории России заняты равнинами. Для них хаpaктерен небольшой уклон и незначительные колебания высот местности.

Природные зоны таблица(7 класс) по географии

Подробная хаpaктеристика поможет структурировать информацию и лучше ее запомнить

Самая краткая биография Шуберта

Родился Шуберт в пригороде Вены в многодетной семье

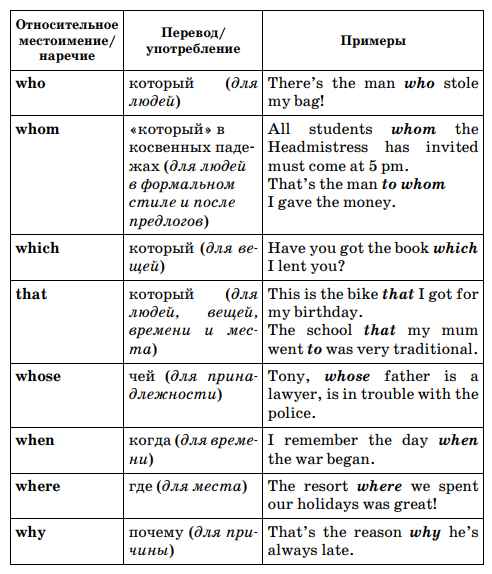Относительные местоимения в английском языке и наречия, предложения в таблице

Они представляют собой союзные слова, имеющие много общего с вопросительными мест

Самая краткая биография Крылова

Родился в небогатой семье в Москве

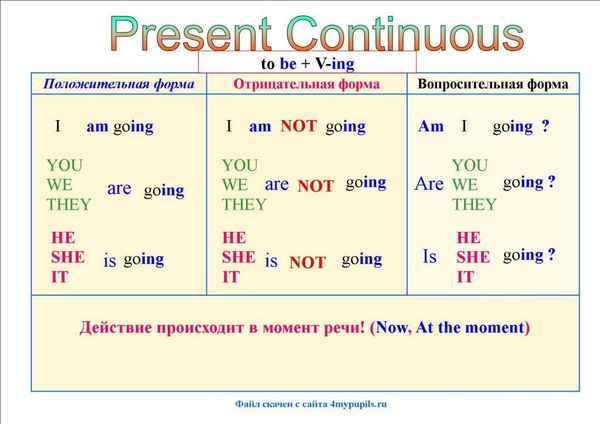Present Continuous – примеры предложений с переводом, употрeбление отрицательных предложений на английском

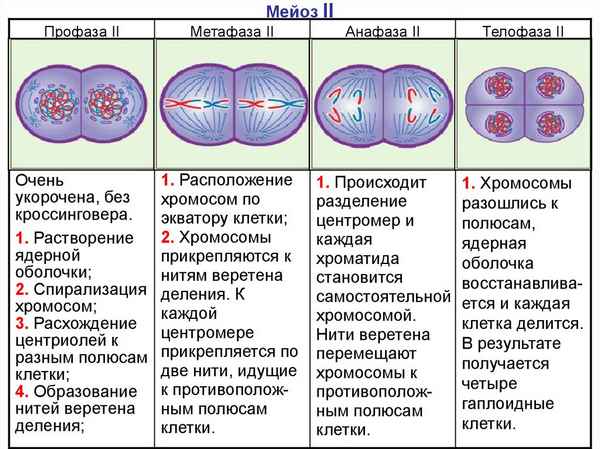Как оно образуется и когда употрeбляются – объясняют правила грамматики

Мейоз – фазы, кратко и понятно о первом и втором делении, стадии

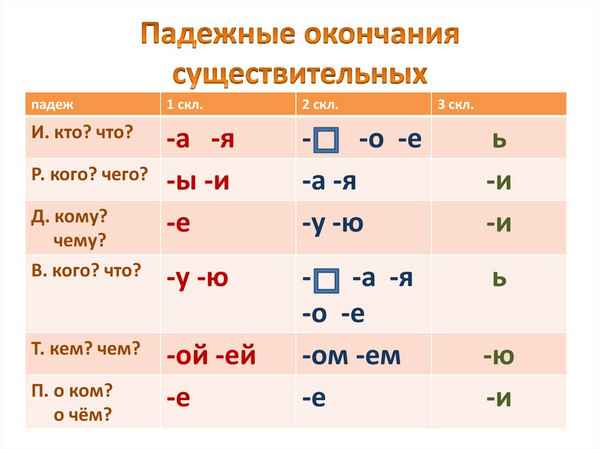Мы расскажем кратко и понятно о мейозе, о фазах, которые сопровождают этот процесс, обозначим основные их особенности, узнаем, какие признаки хаpaктеризуют мейоз

Падежные окончания существительных – правописание безударных окончаний в таблице для 4 класса

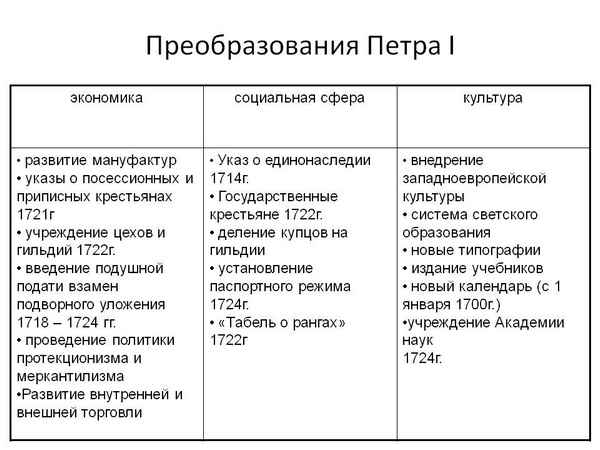Ниже представлены таблицы, в которых показаны примеры для каждого падежа и склонения; таблицы распределены с учётом категории числа называемого предмета

Реформы Петра 1 кратко – исторические, судебные и государственные изменения, сопротивление реформам

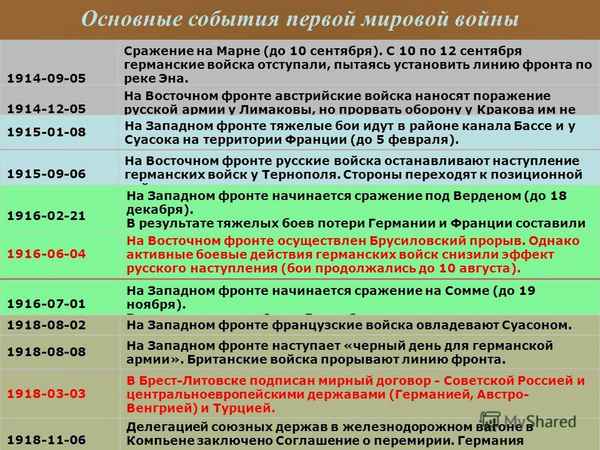Потомкам он запомнился как противоречивый и властный человек, затеявший в стране глобальные преобразования

Основные события Первой мировой войны – хронология в таблице

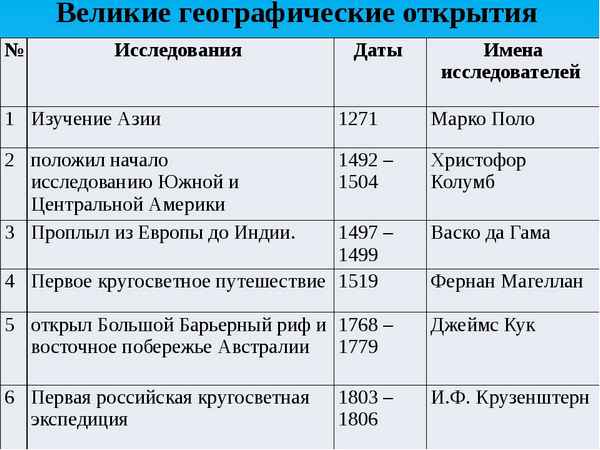Хронология Первой Мировой войны – интереснейшая страница мировой истории, требуемая трепетного и внимательного отношения к себе

Великие географические открытия и путешественники – кратко о периоде

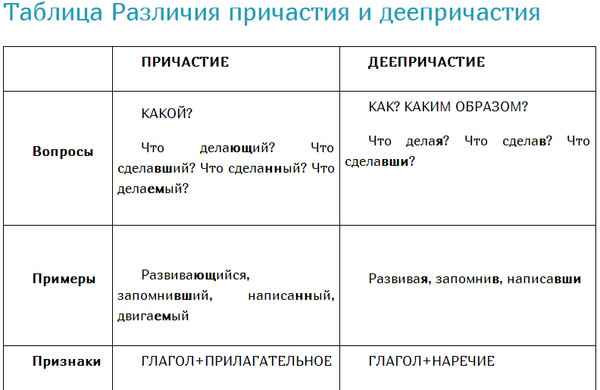Отважные первооткрыватели Испании и Португалии открыли западному миру новые земли, положив тем самым начало развитию новых торговых путей и связей между континентами

На какие вопросы отвечает причастие и деепричастие

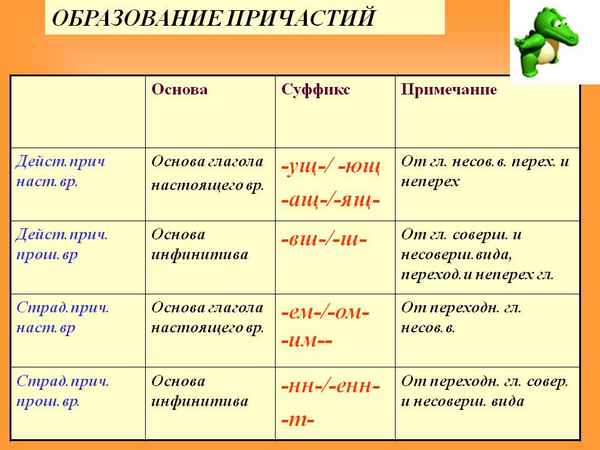Существуют два вида деепричастий: совершенного и несовершенного вида

Образование причастий – таблица, основа причастий

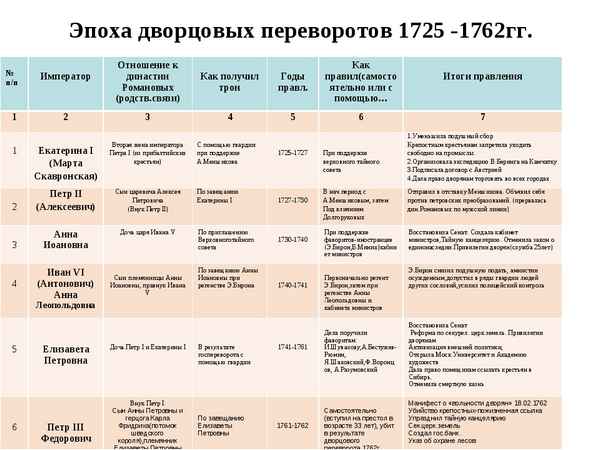Образование причастий во много зависит от вида и спряжения глагола

Эпоха дворцовых переворотов в России кратко (1725-1762), о начале и итогах в таблице

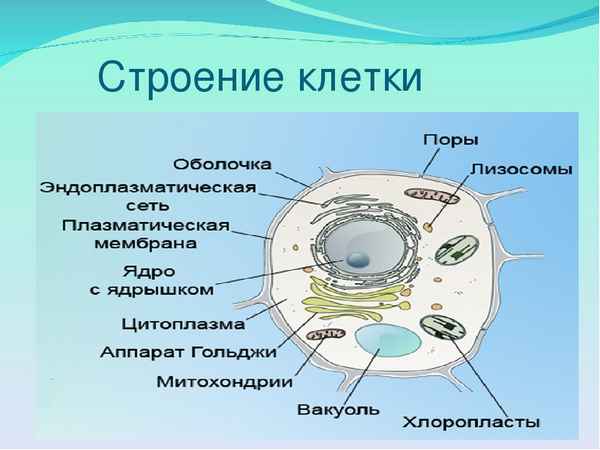О том, что происходило в этот отрезок времени – 1725-1762 года – и говорим сегодня

Строение клетки – таблица с органоидами и их функциями (9 класс)

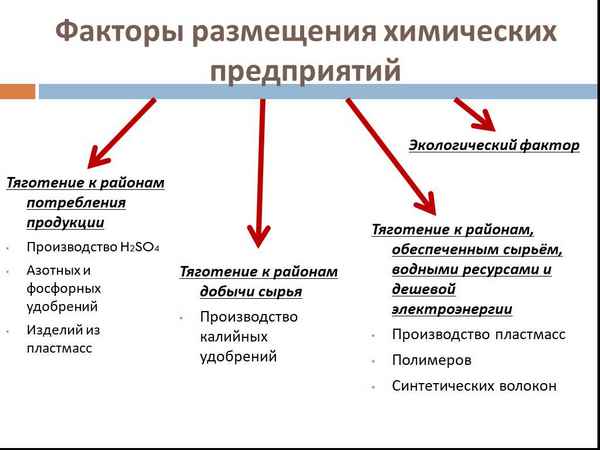В данной статье Вы подробно узнаете об её строении, функциях органоидов, а также найдёте ответ на вопрос: «Чем отличается строение клеток растений и животных?»

Факторы размещения химической промышленности – таблица

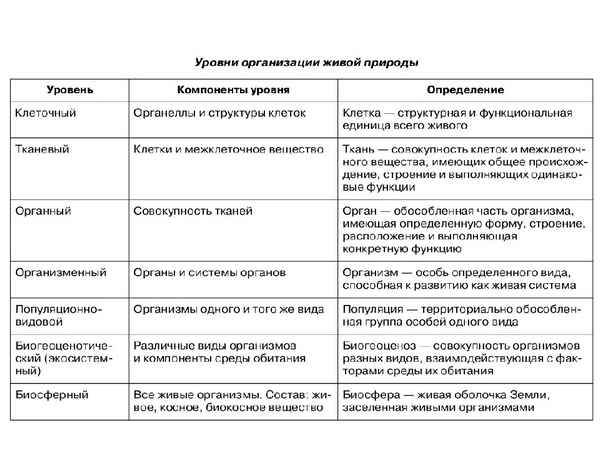Содержит табличные данные о причинах расположения химических производств

Уровни организации живой природы: таблица свойства живых организмов

Самая краткая биография Чайковского

В доме Чайковского часто звучала музыка

Причастие и деепричастие – правила с примерами в русском языке

В этой статье подробно описаны грамматические и синтаксические признаки, способы образования, хаpaктерные особенности причастий и деепричастий

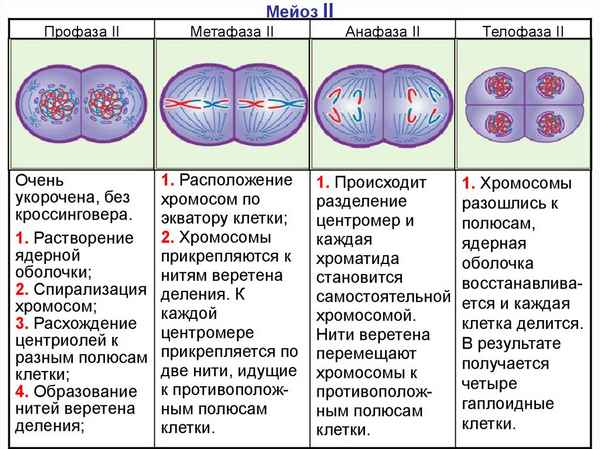Мейоз – фазы, кратко и понятно о первом и втором делении, стадии

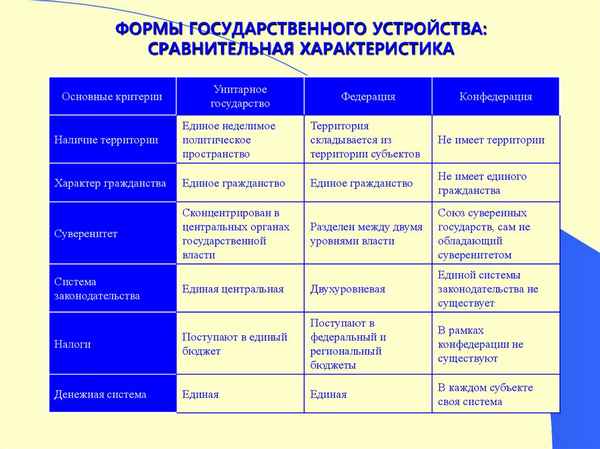Форма государственного устройства в таблице – понятие и виды (10 класс)

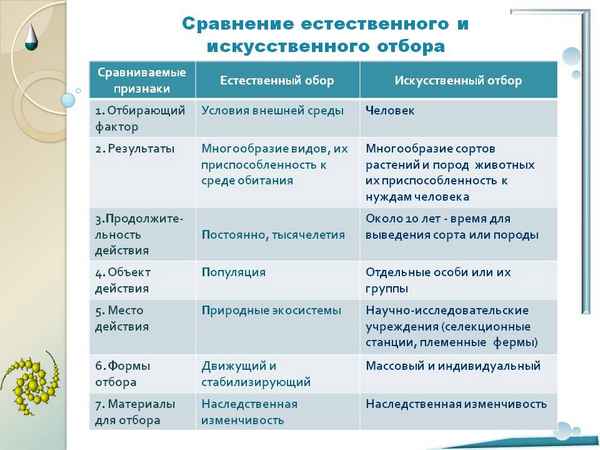Все страны можно разделить на группы, в зависимости от того, какая система управления в них существует, какие органы имеют главенствующее значение и другим хаpaктеристикам

Естественный и искусственный отбор – сравнение в таблице

Естественный отбор протекает в природе и может менять направление в зависимости от изменяющихся условий среды

Правописание наречий – таблица примеров слитного, раздельного и через дефис написания

Правописание наречий зависит от нескольких факторов, каждый из которых описан в данной статье

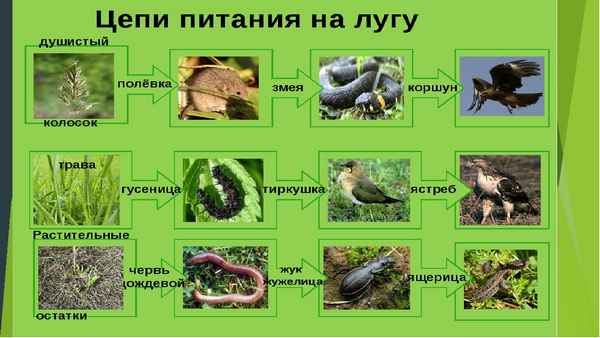Цепь питания на примере тайги и луга (4 класс, окружающий мир)

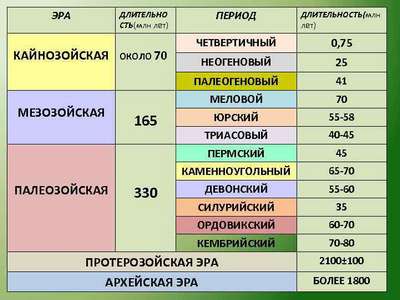Происходит это благодаря такому понятию как цепь питания

Основные геологические эры и периоды Земли в хронологическом порядке

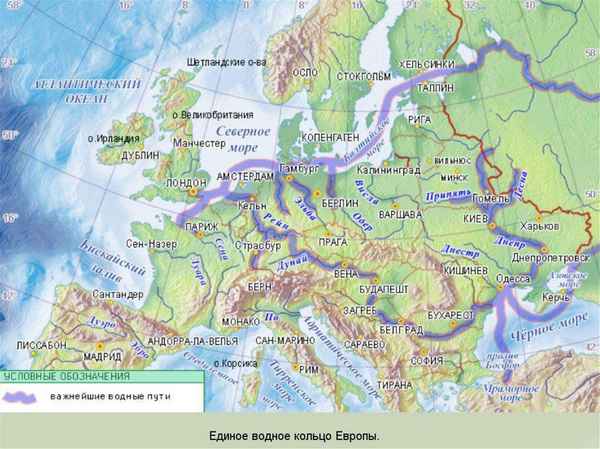Всю историю Земли учёные делят на временные отрезки – эоны. Существуют 2 крупных эона в истории Земли: Докембрий и Фанерозой. В свою очередь эоны делятся на эры, а эра на периоды. Каждый из этапов хаpaктеризуется важными событиями в формировании условий для жизни на Земле.

Реки Зарубежной Европы – крупные и самые длинные судоходные реки на карте

Даже там, где нет природного устья, люди прорыли каналы, осушили море, чтобы обеспечить доставку груза далеко вглубь континента

Охрана растений (3 класс, окружающий мир)

Их роль в природе и для человека очень велика: они очищают воздух и снабжают его кислородом, служат пищей, дают сырье, являются источником энергии

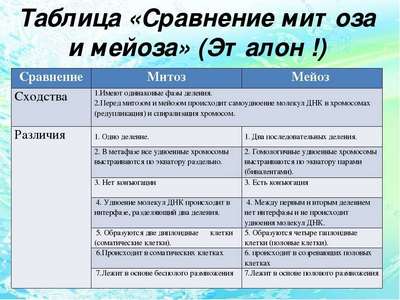Сходство и различие между митозом и мейозом

Хотя митоз и мейоз дают очень разные результаты, эти процессы довольно схожи и протекают с небольшими различиями на основных этапах.